Reasoning on representations learnt by neural networks
Problem
Given a set of entities
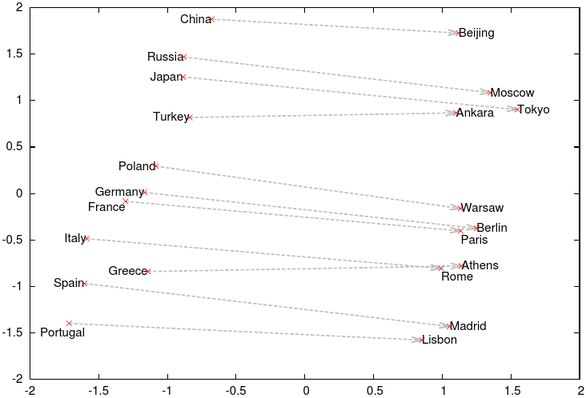
In [1], Tomas Mikolov exhibits figure 1 which nicely shows what Antoine Bordes exploits in [2] : while learning embeddings for words, relations between them appear as translations.
In [2], Antoine Bordes proposes the following model : entities and relations are represented as
A nice example of dataset is Freebase, it shows that a solution to this problem could be used as an inference engine to solve general question/answer.
Solutions
Reimplementation : Link to the repository.
Other transformations
The first tentative was to replace the translation
| Name | Equation | 2D Illustration | Similarity | FB15k | |||
|---|---|---|---|---|---|---|---|
| Micro | Macro | ||||||
| Mean | Top10 | Mean | Top10 | ||||
| Translation | L1 | 233.61 | 36.74 | 361.27 | 32.98 | ||
| L2 | 309.67 | 29.85 | 257.22 | 46.79 | |||
| Cosine | 690.36 | 14.37 | 690.95 | 19.64 | |||
| Point reflection | L1 | 298.27 | 31.91 | 626.19 | 32.00 | ||
| L2 | 419.04 | 23.75 | 582.00 | 39.52 | |||
| Cosine | 1564.66 | 16.43 | 2244.51 | 21.48 | |||
| Reflection | L1 | 249.16 | 29.27 | 269.25 | 29.15 | ||
| L2 | 378.53 | 21.45 | 456.99 | 27.92 | |||
| Cosine | 401.18 | 20.24 | 383.67 | 25.43 | |||
| Offsetted reflection | L1 | 251.96 | 33.26 | 275.61 | 29.51 | ||
| L2 | 431.67 | 20.87 | 412.07 | 28.00 | |||
| Cosine | 408.90 | 20.89 | 328.66 | 30.33 | |||
| Anisotropic Scaling | L1 | 258.74 | 33.91 | 459.69 | 39.71 | ||
| L2 | 550.67 | 18.48 | 1150.81 | 18.89 | |||
| Cosine | 470.64 | 14.41 | 987.91 | 15.36 | |||
| Homotheties | L1 | 400.44 | 23.67 | 627.74 | 27.63 | ||
| L2 | 501.25 | 21.17 | 750.74 | 31.90 | |||
| Cosine | 403.52 | 26.89 | 938.44 | 36.51 | |||
| Anisotropic homotheties | L1 | 268.54 | 32.53 | 472.43 | 39.48 | ||
| L2 | 457.00 | 21.51 | 760.54 | 30.35 | |||
| Cosine | 434.15 | 19.89 | 752.71 | 24.93 | |||
| Element-wise affine | None | L1 | 262.95 | 33.21 | 420.30 | 40.09 | |
| L2 | 417.50 | 22.87 | 692.14 | 32.32 | |||
| Cosine | 401.14 | 21.20 | 738.38 | 26.19 | |||
Where
FB15k is a subset of Freebase with 14951 entities, 1345 relations and 483142 training triplets.
When presented with a training triplet, the left and right score are computed for all 14951 entities, the scores are then sorted and we report as micro mean the mean rank of the correct entity and as micro top10 the percentage of correct entity placed in the top 10. The macro mean is the mean mean rank over all relation : the mean rank is computed for each relation and then the mean over all relation's mean rank is taken (the top10 is defined similarly).
Combining models
The relations in the dataset are hard to analyse since we only have a subset of the graph defining it, however it seems natural that the optimal class of transformation depends on the relation. A first approach was implemented with a product of experts / mixture of models kind of model.
Results :
| Models | Composition | FB15k | |||
|---|---|---|---|---|---|
| Micro | Macro | ||||
| Mean | Top10 | Mean | Top10 | ||
| All L1 | 185.82 | 47.20 | 111.36 | 60.88 | |
Still working on it. See [3].
References
- [1]
- Mikolov, Tomas, et al. "Distributed representations of words and phrases and their compositionality." Advances in Neural Information Processing Systems. .
- [2]
- Bordes, Antoine, et al. "Translating embeddings for modeling multi-relational data." Advances in Neural Information Processing Systems. .
- [3]
- Hinton, Geoffrey E. "Training products of experts by minimizing contrastive divergence." Neural computation 14.8 (): 1771-1800.